Geometry
Areas and perimeters
Geometry started as an attempt to measure the Earth (geo - earth, metry - measurement). Ancient people didn't know the size of the Earth. They didn't even knew the shape of the Earth. Now we know it is a sphere; one of the first evidences for that was the shadow seen during eclipses.
Areas and perimeters:
The perimeter is a path that surrounds an area. From the Greek peri (around - like in peripheral - see more Greek word roots) and meter, that means measure.
For instance, the perimeter of a rectangle is calculated by adding the length of all sides:
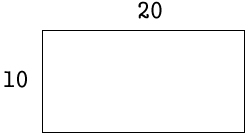
In this case,the perimeter is 2 x 10 + 2 x 20 = 60
The area is the 2 dimensional space inside the perimeter. It is calculated by multiplying the 2 sides of the rectangle. That means 10 x 20 = 200.
It is interesting to note that the same perimeter can enclose different areas:

Now the perimeter is still 60 (2 x 5 + 2 x 25), but the area is 5 x 25 = 75,
The maximum area for a rectangle with a given perimeter is a square:
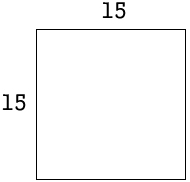
Where perimeter = 60 and area = 15 x 15 = 225
A circle can enclose a larger area than a square, for a given perimeter.
The perimeter of a circle is given by the formula 2 π r, where π is the greek letter Pi.
For a circle to have a perimeter 60, its radius must be: r = 60 / 2 π
= 9.55The area of a circle is given by π r 2, so that in this case it will be 286, considerable more than in the case of the square of the same perimeter, which was 225.
________________________________________________________________________
Now look at this: imagine you break down the original circle in 2. That means, instead of having one circle with a perimeter 60 we make two cicles with perimeters 30 . What would happen to the total area? would it be the same? more? Let's calculate:
For a circle to have a perimeter 30, its radius must be: r = 30 / 2 π
= 4.77 . In that case its area would be π r 2 = 71

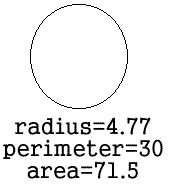
That means that if you make 2 smaller circles, each with half of the perimeter of the original circle, the total area decreases! The areas of the two smaller circles add up to half of the area of the original circle!
And if you go on making even smaller circles you will loose more and more area...
Let's look what happens in the case of spheres >>
© Ricardo Esplugas. 2016
