Unit circle - Animation- I
Helping you to understand SINE
Above you see the unit circle. It has a radius equal 1. Below it, the plot of the sine function, where the value of π (Pi) is assumed to be 3.14 .
The sine function provides the value of the sine of the angle described on the unit circle, by the moving ball.
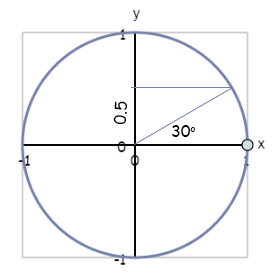
The sine is the projection of the position of the ball on the Y-axis. For instance, when the angle described is 30 degrees (π / 6), the sine is 0.5 (figure). The sine graph is in RADIANS, so that the angles represented on the x-axis are: π /2 (90 degrees), π (180 degrees) and so on.
The projection on the X-axis is the cosine>>
RADIANS AND THE UNIT CIRCLE
The unit circle makes things simple. Remember that the perimeter of the circle is given by the formula 2π*radius. If the radius equals 1, the perimeter is 2π. Therefore, a full circle (360 degrees angle) corresponds to a length of 2π. That is the idea behind radians:
2π radians = 360 degrees
The sine graph shows that sine of 1.57 ( π / 2) = 1. That is what you would expect because π / 2
radians equals 90 degrees, and the projection on the y-axis when the ball is at that angle is 1. Check the other positions!
IMPORTANT: The sine of 90 degrees is 1. The sine of 1.57 is also 1. On the first case the calculation is done in degrees and on the second in radians. THAT IS WHY IT IS CRUCIAL THAT, WHEN YOU USE YOUR CALCULATOR FOR TRIGONOMETRY, YOU SET IT ACCORDINGLY (RADIANS OR DEGREES). Otherwise you may get results a way out.
Now check out the cosine animation>>
