Electric Potential
::Electric potential energy::
The concept of electrical potential energy is analogous to the potential energy concept used in mechanics, where the main examples are gravitational potential energy and elastic potential energy.
If we push a charge in the direction of a fixed charge of the same sign, it is necessary to do work, e.g., to exert a force for a certain distance, in order to overcome the electrical repulsion.If we then let the charge go, it will move by itself because it has stored energy (electrical potential energy). It is similar to pushing an object against a spring.
It is convenient to divide the electric potential energy by the charge. The result is what we call electric potential (or voltage).
That means that 1 volt is 1 joule divide by 1 coulomb.
In the static electricity section we explained that a high voltage is not dangerous if the corresponding current is small. That is because the amount of charges is small and as a result the energy involved, given by the product of the potential times the total charge, is small.
The potential energy of a charge q placed close to a fixed charge Q is given by:
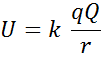
where r is the distance between the two.
To get the electric potential we divide by the charge:
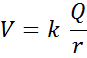
V is the electric potential (voltage) due to the fixed charge Q.
::Examples of calculations ::
1) Two charges, of -2µC and 5 µC , are separated by a distance of 20cm. What is the electric potential in the point in between the 2 charges, at equal distances from both?
The negative charge produces a negative potential, which subtracts from a positive potential.
Calculating the potential at 10 cm from the 5 µC charge:
V = (9*109) *(5 *10-6 ) / 0.1 = 4,5* 105
Calculating the potential at 10 cm from the -2 µC charge:
V = (9*109) *(-2 *10-6) / 0.1 = -1,8 * 105
The total potential at the position is calculated by adding the individual potentials together:
V = 2.7 * 105 volts = 270 kV


