Maths and biology index

Geometry

The size of cells: surface areas and volumes and the shapes of viruses: polyhedra

Probabilities

Mendel´s experiments

Combinatorial analysis

DNA: the four letter code and the independent assortment in meiosis

Sphere calculator*

Input a radius in the field below and you get the volume and surface area of the sphere calculated:

Radius (use at least 1)


Warning: Undefined array key "radius" in /home/scikcul/public_html/advancedpoll/GCSE/biology-and-maths-geometry.php on line 180

Warning: Undefined variable $ratio in /home/scikcul/public_html/advancedpoll/GCSE/biology-and-maths-geometry.php on line 201

radius

Surface area
0

Volume
0

Volume / surface area

 

Maths and Biology - Geometry

Cells

Here I will discuss implications to cells, related to properties of their surface areas and volumes.

As the radius of a sphere increases, the volume increases much faster than the corresponding surface area. You can plug some numbers on the Sphere calculator on the right in order to check that for yourself.

Imagine a unicellular creature, such as a bacterium (plural bacteria). It must get all its oxygen and food through its outer surface. Such membrane acts as an open gut, and also as lungs. In addition, all the waste products must get out via this same membrane.

Interaction of a white blood cell with MRSA*

Let's imagine some spherical bacteria, like MRSA, shown on the left. If their size increased a lot, they wouldn't be able to survive. Geometry explains: the volume would increase much more than the surface area, so that the external membrane wouldn't be able to sustain the flux of nutrients and oxygen that would be needed to feed the much increased internal machinery, that makes up the volume of the bacterium. The same idea also applies to all cells. An elephant is larger than a rat but his cells are about the same size, because cells cannot get large.

There are implications to the size of animals also. A rat is a warm blooded animal, like all mammals. Because it is relatively small for a mammal, it has a relatively large surface area, for its body volume. That is a problem because it will be losing heat through the skin, and the metabolism will have to produce a lot of heat, all the time. Because of this reason, a rat eats about a quarter of its weight every day, and most of this food is used to maintain body temperature. That is also the reason why you don't see rats or other small mammals in the cold regions of the planet.

Virus

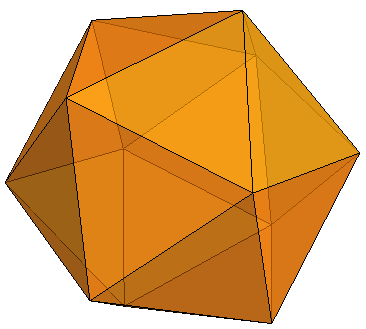
Icosahedral virus*

A virus consist of a protein coat that encloses its genetic material. This coat often have complex geometrical shapes, like in this case above where the protein coat has the form of an icosahedral, shape that possesses 20 sides:

 

 

 

Other polyhedra that are relevant to biology include the protein clathrin, which participates in the formation of vesicles:

electron micrography of the protein clathrin*

 

Radiolaria are protozoa that have a silicon skeleton and live in the sea. They also have complex geometrical structures:

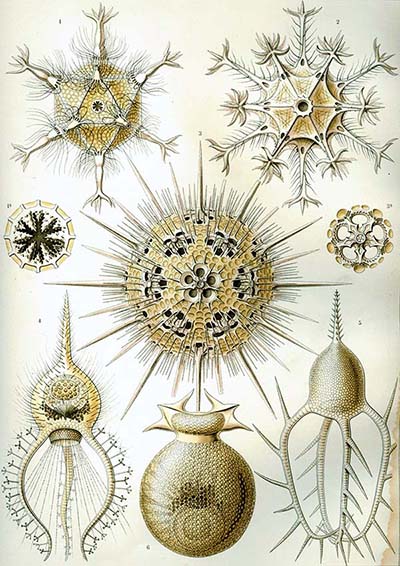
Various radiolaria*

 

* MRSA image is a courtesy of the National Institute of Allergy and Infectious Diseases (NIAID)

*Calculator image  is clip art licensed from the Clip Art Gallery on Discovery

*Icosahedral virus - image by Thomas Splettstoesser  (www.scistyle.com) 

*Wikipedia - clathrin and radiolaria

 

 

NEXT - Probabilities in biology

Mendel´s experiments >>