Specific heat /heat capacity :Examples of calculations
(We consider isolated systems, unless otherwise stated, so that no heat is lost to the environment and the principle of conservation of energy can be applied to work out the answer.)
1) How much heat is needed to raise the temperature of a block of copper ( with mass 0.5 kg) from 0°C to 100° C ? (for copper, c = 386 J / kg oC)
2) How much heat is needed to raise the temperature of 0.5 kg of water from 0°C to 100° C? (for water, c = 4186 J / kg oC)
3)What would be the final temperature of a mixture of 100 g of water at 90°C and 600 g of water at 20°C ?
4)What would be the final temperature if a 2 kg piece of lead at 200°C is inserted in a container with 10 kg of water at 50°C ? (for lead, c = 128 J / kg oC)
5) Two equal recipients A and B, with 2 different liquids, initially at 20°C, are heated by a hot plated and both receive the same amount of heat. As a result, the temperature of liquid A is raised to 40°C and that of liquid B is raised to 80°C. If the liquids are removed from their recipients and mixed, the final temperature would be around:
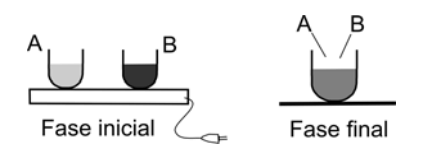
a) 45°C b) 50°C c) 55°C d) 60°C e) 65°C
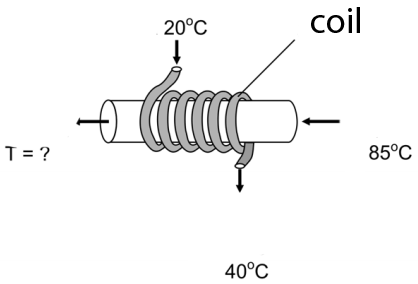
6) A heat exchanger consists of a coil shaped pipe wraped around a wider pipe.The water in the coil is used to cool the water on the main pipe and it has a flow rate of 18 l /s ; it enters at 20ºC and leaves at 40 ºC (as shown on the image). The water on the main pipe has a flow rate of 18 l/s. If it enters at 85ºC, what will be its exit temperature?
a) 75 ºC b) 65 ºC c) 55 ºC d) 45 ºC e) 35 ºC
Examples involving melting ice are a bit more tricky and can be found here: exercises involving also latent heat>>
example - 9/11 physics- how much heat needed to weaken the towers?
Answers:
1) Applying the formula:
![]()
Q = 386 * 0.5 * 100 = 19300 J or 19.3 kJ
Comments: It is important to observe the SI units. The mass is in kg and the heat energy in J. Normally the temperature is converted into K, but because we are taking the difference (or the variation), it doesn't matter what units are used (if kelvin or celsius). However, if the difference of temperatures can be plugged in the formula in the scales kelvin or celsius (no need to convert celsius into kelvin). If the difference is in degrees farenheit a conversion (to celsius or kelvin) is needed before using the formula.
2) Q = 4186 * 0.5 * 100 = 209300 J or 209.3 kJ
Comments: Note that this is more than 1o times the nergy needed in the case of copper!
3) This example is also typical and it requires some algebraical skills.
We know that heat flows from the hotter body to the cooler body. Hence, the water at the higher temperature will "loose" heat and the water at the lower initial temperature will "gain" heat. The correct way of describing this situation is by saying that heat will be transferred from the hotter to the cooler water.
We also know that, by conservation of energy, the amount of heat lost will be the same that is gained.
So, let's call the final temperature of the mixture Tf.
The amount of heat that will be transferred from the hotter water is:
4186 * 0.1 * (90 - Tf)
The amount of heat that will be transferred to the cooler water is:
4186 * 0.6 * ( Tf -20)
Because these two quantities must be equal, we have an equation:
4186 * 0.1 * (90 - Tf) = 4186*0.6 * (Tf - 20)
We need to find Tf:
418.6 * (90-Tf) = 2511.6 * (Tf-20)
Getting rid of the brackets:
37674 - 418.6 Tf = 2511.6 Tf - 50232
-2930.2 Tf = -87906
Tf = 30° C
4) Similar to 3) above,
in this case:
amount of heat transferred from the lead:
128*2*(200-Tf)
amount of heat transferred to the water:
4186*10*(Tf-50)
Equating the two heats:
128*2*(200-Tf) = 4186*10*(Tf-50)
256(200-Tf)=41860(Tf-50)
51200-256 Tf = 41860 Tf - 2093000
42116 Tf = 2144200
Tf = 50.9°
5) This is a very good problem and I will provide an extended answer.
Initial considerations:
Both liquids receive the same amount of heat but liquid B achieves a higher temperature. That means that liquid A requires more heat in order to raise its tempearature. In other words, liquid A has a specific heat that is higher than the specific heat o liquid B.
Then, the heat source is removed and the liquids are mixed. What is the final temperature? It is temptaing to guess 60 ºC because that is half way between the 2; that would be correct if both liquids had the same specific heat, but that is not the case as we know the A has a higher specific heat. Because of that, the heat transferred from liquid B (that is hotter) cannot raise the temperature of A very much.
So, these intial considerations enable us to eliminate some answers. The final temperature must be lower than 60 ºC.
Calculations
-Parte 1
Both liquids receive the same amount of heat so QA= QB:
QA = cA mA ΔT = cA mA (40-20) = cA mA*20
QB = cB mB ΔT = cB mB (80-20) = cB mB*60
Equating both formulas:
cA mA*20 = cB mB*60 ==> cA mA = 3 cB mB (I)
-Parte 2
The final temperature (Tf) achieved when the liquids are mixed up must be intermediate between the two. The hotter one will lose heat that will be gained by the other. This amount of heat must be equal because no heat is lost to the environment and energy must conserve. Based on that we can write another equation:
(80 - Tf ) cB mB = (Tf-40) cA mA
Using (I):
(80 - Tf ) cB mB = (Tf-40) 3 cB mB
Tf = 50 ºC
Answer is b)
OBS: Perceba que as massas e calores específicos dos líquidos não foram dadas porque seriam canceladas durante os cálculos.
6) This heat exchanger calculation is typically performed in chemical or mechanical engineering practice.
Let´s consider what happens during 1 min:
-Part 1
We call Q1 the heat received by the water in the coil. The specific heat of water is represented by c and the density of water is 1 kg/l as usual.
It is heated from 20ºC to 40ºC hence ΔT=20 :
Q1 = 18 *c *20 = 360 c
-Part 2
We call Q2 the heat lost by the mater on the main pipe. It is cooled from 85ºC
to a final temperature Tf which we must calculate:Q2 = 12 * c * (85 - Tf)
-Part 3
The heat lost by the water in the tube must equal the heat gained by the water in the coil, so taht:
Q1 = Q2
360 c = 12 (85 - Tf) c
Cancelling c:
360 = 1020 - 12 Tf
-660 = -12 Tf
Tf = 55 ºC
OBS:The specific heat of water was not provided because it would be cancelled anyway.
exercises involving also latent heat>>
example - 9/11 physics- how much heat needed to weaken the towers?


