Questões de vestibular e concursos públicos
Raciocínio Lógico - II
Diagramas de Venn
Respostas
1) (2014) Prova: Agente de Polícia Judiciária - Substituto
Num grupo de 120 pessoas sabe-se que 72 gostam de jogar basquete, 65 gostam de jogar futebol e 53 gostam dos dois. Nessas circunstâncias, é correto afirmar que:
a) 21 pessoas gostam somente de jogar basquete.
b) 14 pessoas gostam de jogar somente futebol.
c) O total de pessoas que gostam de somente um dos dois é igual a 33.
d) 36 pessoas não gostam nem de basquete e nem de futebol.
Primeiro vamos desenhar o diagrama e preencher com os números fornecidos:
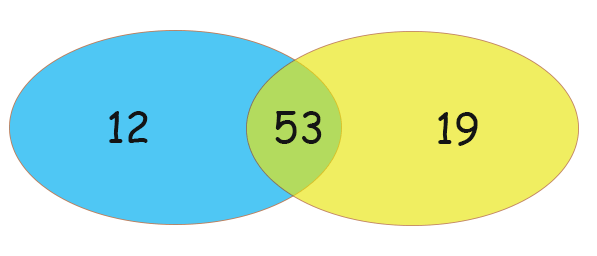
O conjunto azul representa os que gostam de futebol e o amarelo os que gostam de basquete. Na intersecção temos os que gostam dos 2 , que são 53 pessoas.
Observando o diagrama podemos responder todas as perguntas, por exemplo, quantos gostam só de futebol? Resposta: 12. Vemos também que 19 gostam só de basquete.
Vemos também que 84 gostam de futebol ou basquete (somando-se todos os números).
Como temos 120 pessoas, pode-se concluir que 36 não gostam nem de futebol e nem de basquete (alternativa d).
Sim, perceba como os dois balõezinhos acima deixam tudo mais fácil... Veremos agora problemas com mais balõezinhos...
2) ( 2014) Prova: Agente Administrativo
Numa pesquisa realizada com 100 pessoas sobre a forma de se locomoverem para o trabalho, constatou-se que:
• 45 usam ônibus;
• 51 usam automóvel;
• 32 usam moto;
• 18 usam ônibus e automóvel;
• 22 usam ônibus e moto;
• 15 usam automóvel e moto;
• 6 usam os três meios de transporte.
Analisando os dados apresentados, conclui-se que o número de pessoas que NÃO utiliza nenhum dos três meios de transporte mencionados é
a) 17.
b) 21.
c) 23.
d) 26.
Primeiramente desenhamos os 3 conjuntos de forma que possamos preencher com números as áreas de intersecção entre eles. Agora começamos a preencher. Eu costumo preencher primeiro os números que estão em preto.
Preenchemos com o número 6 o espaço onde há a intersecção dos três, pois 6 pessoas usam os 3 transportes:
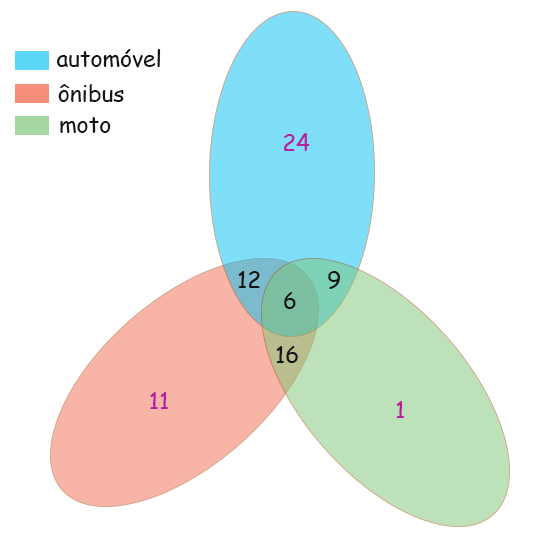
Sabemos que 15 usam automóvel e moto, portanto a intersecção destes 2 conjuntos deve ter 15. Como já estão lá os seis que usam todos os transportes (e portanto usam automóvel e moto), só falta adicionar 9. Da mesma maneira preenchemos os outros números pretos.
Para preencher os números roxos, procede-se assim: existem 32 que usam moto e já há 31 no conjunto verde. Quer dizer que tem que adicionar mais um no verde (que é o número 1 que se vê em roxo). Da mesma forma preenche-se o resto do diagrama.
Pronto! Com o diagrama completo, pode-se responder qualquer pegunta. Por exemplo, quantas pessoas usam só moto? Resposta:1.
No caso a pergunta é quantas pessoas não usam nenhum desses transportes. Somamos todas as pessoas que usam estes transportes - todos os números no diagrama- o que dá 79. Temos 100 pessoas e portanto 21 não usam nenhum desses transportes. Resposta b.
3) 2015 - SEGPLAN-GO - Perito Criminal
Suponha que, dos 250 candidatos selecionados ao cargo de perito criminal:
1) 80 sejam formados em Física;
2) 90 sejam formados em Biologia;
3) 55 sejam formados em Química;
4) 32 sejam formados em Biologia e Física;
5) 23 sejam formados em Química e Física;
6) 16 sejam formados em Biologia e Química;
7) 8 sejam formados em Física, em Química e em Biologia.
Considerando essa situação, assinale a alternativa correta.
a) Mais de 80 dos candidatos selecionados não são físicos nem biólogos nem químicos.
b) Mais de 40 dos candidatos selecionados são formados apenas em Física.
c) Menos de 20 dos candidatos selecionados são formados apenas em Física e em Biologia.
d) Mais de 30 dos candidatos selecionados são formados apenas em Química.
e) Escolhendo-se ao acaso um dos candidatos selecionados, a probabilidade de ele ter apenas as duas formações, Física e Química, é inferior a 0,05.
Primeiramente prepara-se o diagrama. Preenchemos como no problema anterior, de modo que obtemos o seguinte:
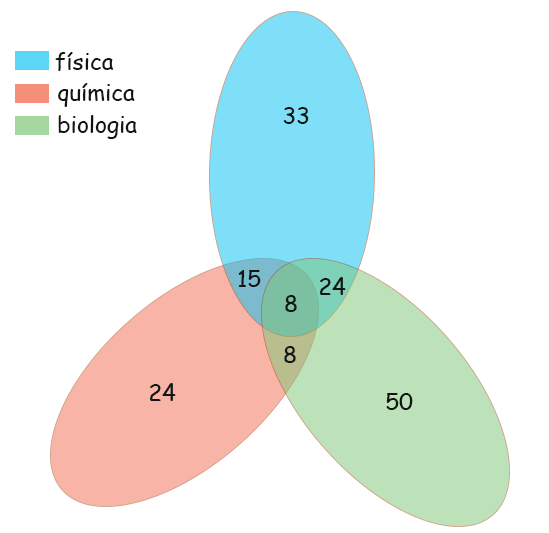
Agora vamos examinar as opções:
a) Temos 250 candidatos no total. Os números no diagrama (que representam todos os biólogos, químicos e físicos), somam-se produzindo um total de 162. Portanto 88 pessoas não são nem biólogos, nem químicos ou físicos. Alternativa correta.
b) Temos 33 formados apenas em física. Alternativa errada.
c) Temos 32 formados em física e biologia. Alternativa errada.
d) Apenas 24 são formados apenas em química. Alternativa errada.
e) 23/250 = 0.092. Alternativa errada.
Comentário: Perceba que para escolher a alternativa e) não precisava-se ter feito todo esse trabalho de desenhar o diagrama , etc. Bastava dividir 23 por 250.
4) e)
5) b)
Raciocínio lógico - índice de capítulos>>
