Electric Circuits
Any path set for the flow of electrons is called aan electric circuit. There are 2 basis types: series circuits and parallel circuits.
In a series circuit the same current goes through the whole circuit, whereas in a parallel circuit the total current divides to go different branches of the circuit, and then it get together again.
This article refers to circuits containing only batteries and resistors. Various devices are eqivalent to a resistor, namely light bulbs, buzzers, motors, etc.
(The light bulbs in all the examples below are equal )
::Series Circuit::
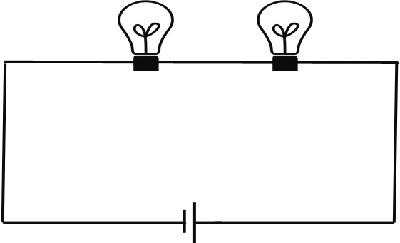
In this case, the same current flows in both light bulbs, so that they both will shine with the same intensity.
Let's suppose that the resistance of the bulbs is 50 ohms and that the battery provides 12 V. Before we use Ohm's Law, we calculate the total resistance of the circuit (the resistance of the wires is ignored). This is the sum of the individual resistances, in this case 50+50 = 100 ohms. This sum is also called the equivalent resistance of the circuit.
U=RI --> 12 = 100 I --> I = 0.12 A
::Parallel Circuit::
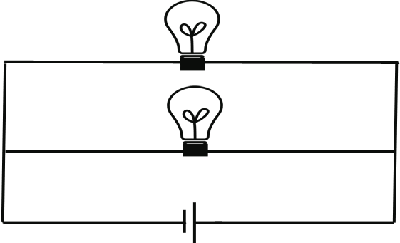
In this case the current splits into two components. Because both bulbs are equal the currents splits into 2 equal components.
The calculation of the equivalent resistance ( Req )in this case is different; the following formula is used:
1 / Req = 1 / R1 + 1 / R2 + ....
so that all resistances in parallel are included. In this case there are only 2, so:
1 / Req = 1 / 50 + 1 / 50 --> Req = 25 ohms
NOTE: This calculation illustrates a general rule: when 2 equal resistances are in parallel, the equivalent resistance is half of the value of the individual resistance!
Using Ohm's LAw with this resistance:
U = RI --> 12 = 25 I --> I = 0.48 A
Notice that the current in this case is 4 times higher than in the case of the same resistances in series.
What happens if we add an extra light bulb in parallel? would the current increase even more?
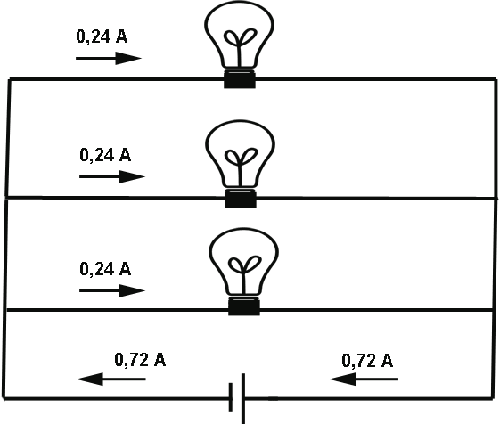
3 light bulbs in parallel
In this case the equivalent resistance will be:
1 / Req = 1 / 50 + 1 / 50 + 1 / 50 --> Req = 16.67 ohms
12 = 16.67 I --> I = 0.72 A
So yes, the current increases even more in this case!
The image below shows how the total current in this circuit (0.72A) splits equally in the 3 branches:
::Question::
Two light bulbs , with resistances R1 and R2, are part of two different circuits:
a) parallel
b) series
Which is the brightest light bulb in each case?
Note: the brightest bulb will be the one submitted to the highest current.


