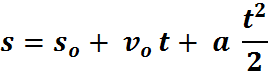Kinematics II - Graphs as an aid for problem solving
d x t graphs
It is the study of motion. Kinos (from Greek) means movement. The word cinema comes from kinema (moving images). Kino means cinema in German.
The use of graphs can make easier the problem solving process. In here I will show graphs that occur in the field of kinematics, and also discuss relevant mathematical concepts like the gradient.
The basic concepts in kinematics are described in a previous page. I will only repeat here that:
The velocity is the gradient of the d x t graph
Velocity is the speed in a given direction. It may be negative!
Example 1
 This is a d x t graph so that its gradient is the velocity. The gradient is the slope of the graph.Mathematically it is calculated easily because it is the tangent of the angle α (alpha), so that it is given by the opposite side of the triangle (20 -the height of the red line) divided by the adjacent side (10). That is:
This is a d x t graph so that its gradient is the velocity. The gradient is the slope of the graph.Mathematically it is calculated easily because it is the tangent of the angle α (alpha), so that it is given by the opposite side of the triangle (20 -the height of the red line) divided by the adjacent side (10). That is:
v = d / t = 20 /10 = 2 m / s
_____________________________________________________________
Example 2
v = 40 / 5 = 8 m / s
_________________________________________________________
Example 3
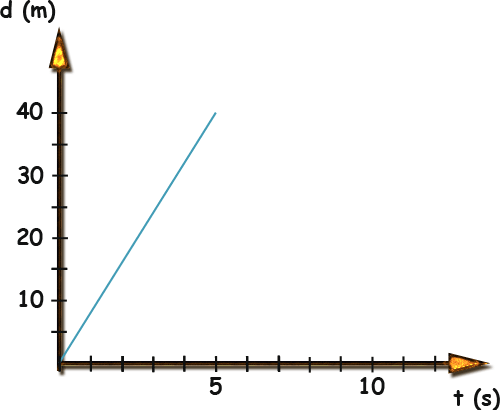
I - 5 m/ s
II - 0
III - 15 /5 = -3 m/s
Explanation: Here there are 3 different gradients. In II the gradient is zero (there is no slope) . In III, the angle α is larger than 90 degrees, so that the tangent (and as a result the gradient) is negative.
__________________________________________________________
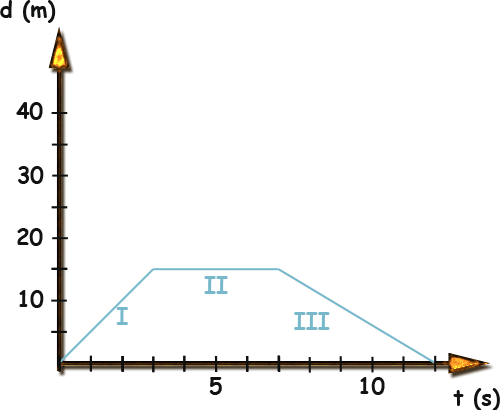
Example 4
Calculate yourself the velocities in this case!
Now look at the v x t graphs>>
© Ricardo Esplugas. All images in this site can be bought in an enlarged version. Please contact me on ricardochemistry@gmail.com