Doppler Effect
This is a very interesting and important effect. It was discovered by the Austrian physicist Christian Doppler in 1842. It has been crucial for astrophysics and cosmology and it is also applied in medicine, aviation, etc etc... It is also used by dolphins!
The typical example is the sound you hear from an ambulance, with its noisy siren, that approaches you and then moves away. The frequency of the sound you hear is higher when the ambulance is approaching and it is lower when it is moving away. This variation of frequency, as a result of the movement between the source of the sound wave and the receiver, depends on the relative velocity: the higher the relative velocity, the higher the frequency variation. This idea can be represented by a simple formula:
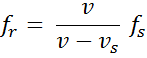
fr = frequency received, fs = frequency of the source, v = velocity of the wave and vs = velocity of the source (it is positive when source and receiver are approaching each other and negative if they are moving away from each other).
It is expected a positive velocity when objects approach each other, because in that case the fraction will have a value larger then 1 and as a result fr > fs as you would expect. And vice-versa.
EXAMPLE
Let´s apply the formula above to the ambulance example. Suppose the ambulance is travelling towards you with a velocity of 50 m/s and emitting a 300 Hz sound. What sound frequency will you receive? (the speed of sound waves in air is 343 m/s)
Answer:
fs = 300 Hz, vs = 50 m/s, v = 343 m/s (important: the numbers must be in these units used here )
fr = (343 / 343-50) 300 = 1.17* 300 = 351 Hz
The following images will illustrate the concept of Doppler Effect.
Imagine water drops falling into a pond, so that you get those familiar ripples in the water (λ is the wavelength):
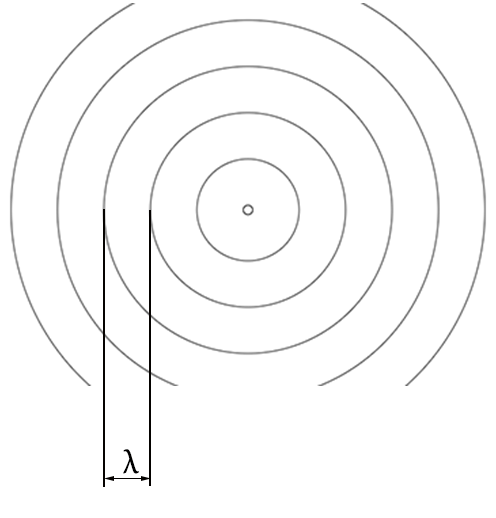
Any observer around will detect the same wavelength λ.
Now imagine that the source of the water drops start moving to the left, so that you will see that:
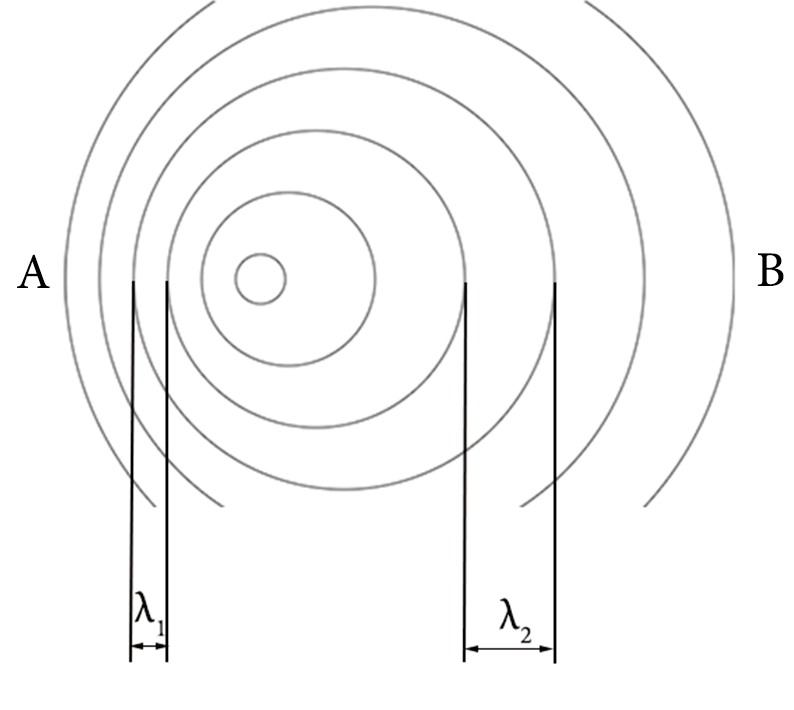
An observer at A detects a wavelength λ1 which is smaller than the wavelength λ2 detected by an observer at B. Remember that a smaller wavelength corresponds to a higher frequency.
λ1 < λ < λ2
This images were produced using my Doppler effect simulation, which you can also use. Try varying the velocity to obtain different patterns.
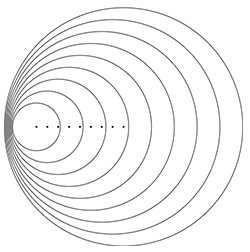
It is interesting to notice that the distance between the centres of the circular waves gives an idea of the velocity at which the wave source moves:
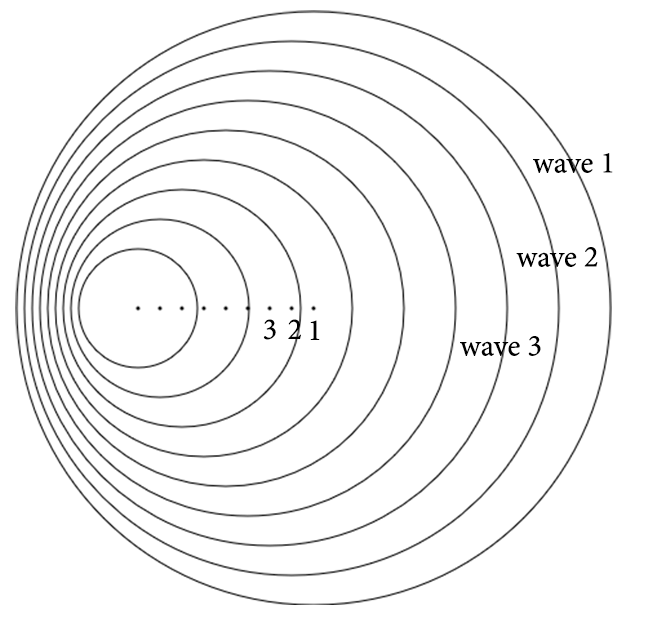
This image was produced using the static simulator. Play with it. Try different velocities for the wave source!
Bow Waves
If you have been playing with the Doppler effect simulators, you must be curious about what happens when you choose a high velocity.
If the velocity of the wave source is too high, it can be higher than the velocities of the waves it emits! In this case we get a cone shape:
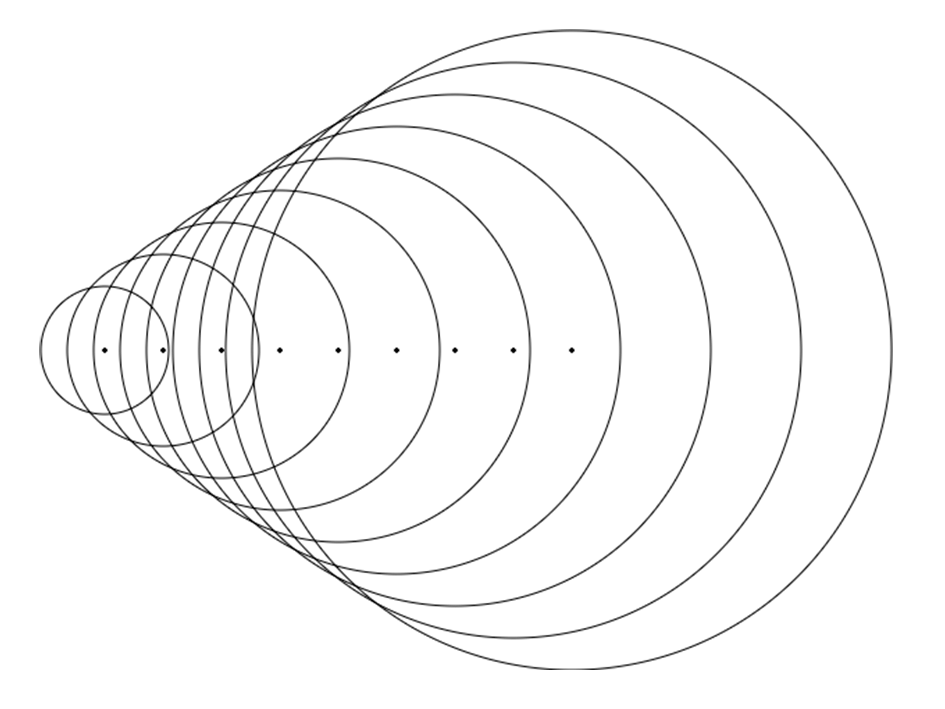
That is what happens, for instance, when an aircraft breaks the sound barrier. Fighters can travel faster than the speed of sound and produce this kind of waves.
You can also see this V-shaped pattern when you observe the waves produced at the rear end of a motorboat.