Polígonos - Fórmulas
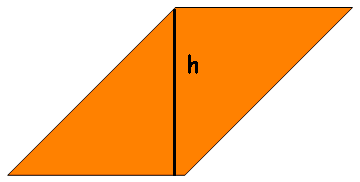
A altura é a linha que sai de um vértice e é perpendicular ao lado oposto, onde ela termina. Costuma ser representada pela letra h (height-altura em inglês).
Fórmulas de áreas de polígonos
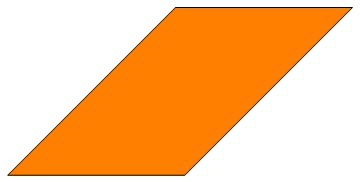
Paralelogramos
quadrado
retângulo
paralelogramo
(caso geral)
Área = b x h (base x altura)
Perceba que o retângulo e o quadrado são casos particulares do paralelogramo, o qual tem lados paralelos alternados. O retângulo é um paraleogramo com ângulos retos e o quadrado é um retângulo com os lados iguais. A área do retângulo é apenas o produto dos dois lados (e no quadrado um lado elevado ao quadrado).
A altura do paralelogramo é representada abaixo:
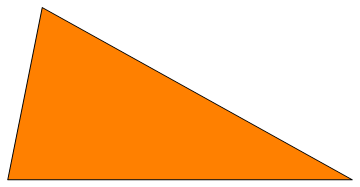
Triângulos
acutângulo
(todos os ângulos menores de 90)
retângulo
(1 ângulo igual a 90)
obtusângulo
(1 ângulo maior que 90)
Percebam que não dá pra ter mais de um ângulo maior ou igual a 90 porque a soma dos ângulos internos do triângulo é sempre igual a 180.
Área = b x h / 2
Isto porque a área do triângulo corresponde à metade da área do parelelogramo que poderia ser construído traçando-se lados paralelos aos do triângulo.
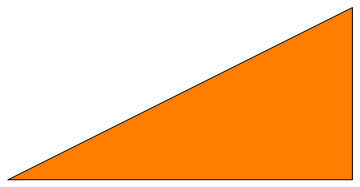
A altura do triângulo retângulo será igual ao lado perpendicular à base, nesta posição em que o vemos. Se o triângulo for virado em outra posição a altura será outra. Existe uma altura diferente para cada um dos lados. Apenas no caso do triângulo equilátero (todos os lados iguais) as alturas serão todas iguais.
Altura no caso do triângulo obtusângulo.
Área do triângulo equilátero
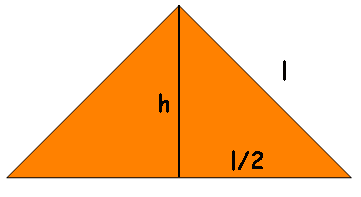
Chamando-se o lado de l , aplicamos o Teorema de Pitágoras para determinar o valor da altura (h):
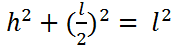
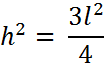
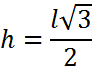
Agora pode-se aplicar A = b x h / 2:
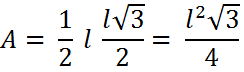
Este é um resultado bastante útil. É usado em diversos problemas de geometria, incluindo o cálculo da área do hexágono regular (abaixo).
Trapézios
Área = (B+b) x h / 2
Onde B é a base maior (nesse caso a base inferior) e b é a base menor (nesse caso a base superior).
Essa fórmula pode ser deduzida dividindo-se o trapézio em dois triângulos:
Ambos triângulos têm a mesma altura, que é a altura do trapézio. A área do triângulo superior é b x h / 2 e a do inferior B x h / 2. Somando-se as áreas dos dois obtem-se a formula acima.
Alternativamente, o trapézio pode ser calculado como se fosse um retângulo com um triângulo à esquerda e outro à direita.
Área = b x h / 2
Hexágono regular
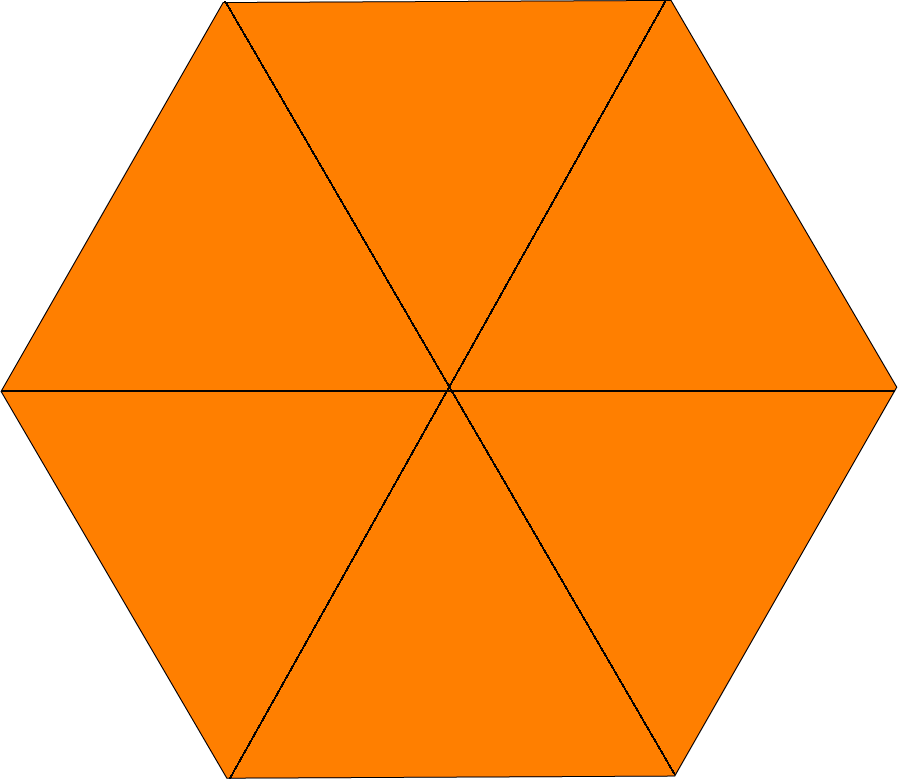
Caso o comprimento dos lados seja conhecido, área do hexágono regular (todos os lados iguias) pode ser calculado dividindo-o em 6 triângulos equiláteros.
Considerando-se que cada lado do hexágono tenha medida l, basta somar a área dos 6 triângulos equiláteros (calculadas acima), e o resultado será:
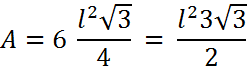
Losango
O losango pode ser tratado como um paralelogramo.
Outras fórmulas para cálculo de áreas de triângulos:
Em alguns casos pode ser difícil aplicar a fórmula tradicional para a área do triângulo, e pode ser conveniente usar as fórmulas alternativas abaixo:
Lembramos que o semiperímetro - p - corresponde à metade do perímetro, que é a soma dos comprimentos dos 3 lados:
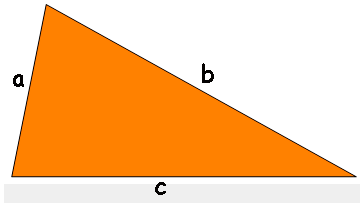
p = (a+b+c) / 2
1) Com base nos comprimentos dos lados
2) Com base em p e no raio da circunferência inscrita (r)
A = p r
3) Com base no comprimento de dois lados e o ângulo entre eles (Â)
A = b c sen  / 2
4) Com base nas medidas dos lados e do raio da circunferência circunscrita(R)
A = abc / 4R
Outras fórmulas importantes:
Soma dos ângulos internos:
n = número de lados do polígono
Número de diagonais:
(As diagonais são linhas que unem vértices não adjacentes)
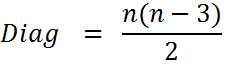
Lei dos cossenos
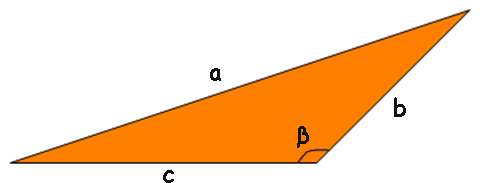
Esta fórmula permite calcular o lado a quando se conhecem os lados b e c e o ângulo β:
a2 = b2+ c2 -2 b c cos β
Perceba que esta fórmula é mais geral do que a do Teorema de Pitágoras, pois aplica-se a qualquer ângulo β. Caso o ângulo seja reto, cos 90 = 0 e portanto a forma torna-se a de Pitágoras. No caso de um ângulo obtuso, como na figura acima, cos β < 0 e portanto um termo será adicionado ao que seria o valor de a no caso do ângulo reto, como seria de se esperar, pois o lado a será comprido. Se o ângulo fosse agudo, cos β >0 e um termo seria subtraído.
Lei dos senos
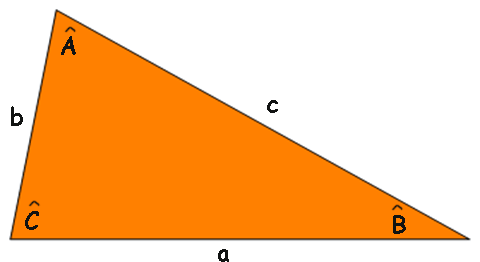
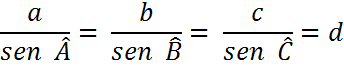
Quer dizer que, em qualquer triângulo, o quociente da medida de cada lado pelo seno do ângulo oposto a ele é constante. Essa constante de proporcionalidade (d) corresponde ao diâmetro da circunferência circunscrita a esse triângulo.