Transition Metals
Crystal field theory
According to crystal field theory (CFT), which is based on electrostatic interactions the behaviour and geometry of transition metal complexes is determined by the number of d electrons present in the system.
In this section the basic consequences of CFT will be discussed briefly. In CFT the metal and the ligands are treated as point charges. A free metal atom or ion has five degenerate d orbitals, whose appearance is shown in figure 2.1. When other atoms or molecules approach the metal centre, the degeneracy of its d orbitals is lifted. The way in which their energies change will depend on these orbital shapes and on the directions from which the ligands approach them.
d orbitals
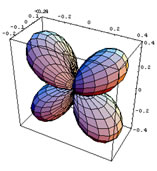
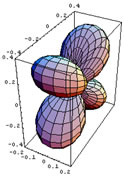
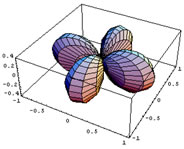
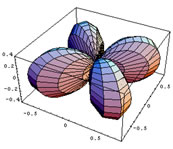
Figure 2.1 is a representation of the five hydrogenoid d orbitals.
The first three orbitals shown on figure 2.1 have their lobes in between the cartesian axes, and the last two have their lobes on the axes. The orbital is aligned with the z-axis and the dx2- y2 has lobes along the x and y axes.
 |
|
|
dxy |
dxz |
dyz |
|
|
dz2 |
dx2- y2 |
Figure 2.1: Hydrogenoid d-orbitals.
Knowing the shapes of each d orbital, it is simple to figure out qualitatively in which way their energies will shift in the presence of a crystal field of a given geometry if only electrostatic interactions are to be taken into account. The Oh and Td geometries will be studied first. Next, the D4h case will be analyzed as a distortion of the Oh geometry. In each case, the degenerate unsplit d orbital energy is taken as zero.
The octahedral crystal field
In this geometry, the ligands will approach the metal along all three axes. It means that the orbitals that lie along the axes and dx2- y2 will have their energy increased due to electrostatic repulsion, whereas the other three orbitals will have their energies lowered. Two ligands will approach along the z-axis and the other four will approach along the x and y axes.
It is easy to understand why the two orbitals mentioned above have their energies increased, but it is not as clear why the energy of the other three is lowered. This lowering happens in order to preserve the “centre of gravity” of the levels . In order to do so, the sum of all orbital energies must be zero and some orbitals acquire negative energies to compensate for the positive energies acquired for the orbitals that are repelled. This rule only works when the interactions are considered to be purely electrostatic. Hence, the d orbitals in an octahedral complex will split in the manner shown in figure 2.2:

Free metal (left) |
Metal in an octahedral field (right) |
Figure 2.2: Ligand field splitting diagram for a transition metal in an octahedral geometry.
The energy difference between the new sets of levels is called crystal field energy (CFE) and is commonly represented by the Greek letter Delta.
The tetrahedral crystal field
In the tetrahedral case, the ligands approach in directions that are at 45 degrees from the main axes. It means that they come from the direction of the vertices of the boxes drawn around the orbitals in figure 2.1. In this case, the orbitals that are going to be repelled are the ones that are represented at the top of figure 2.1, i.e., the, and . The other two orbitals, and dx2- y2 will be lowered in energy as shown in figure 2.3.
It is important to note that the CFE associated with the tetrahedral geometry is smaller than in the octahedral case.
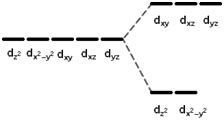
Free metal (left) |
Metal in a tetrahedral field (right) |
Figure 2.3: Crystal field splitting diagram for a transition metal in a tetrahedral geometry.
The square planar crystal field
In order to find out what the ligand field splitting in the square planar geometry is, it is convenient to start from the octahedral splitting (figure 2.2). The square planar geometry can then be considered as a deformation (elongation) of the octahedral geometry, which will occur along the z-axis. The z-axis contains the two axial atoms (top and bottom of the octahedron), so that four atoms stay in position and the symmetry can be lowered to D4h. This will lift the degeneracy of most orbitals.
The dx2- y2 orbital will still be high in energy, but the orbital will be stabilised, because there are no more ligands in this direction. Due to the breaking of the Oh symmetry, the three orbitals at the bottom of the Oh diagram will no longer be degenerate. One of them - the one along the xy plane - will acquire a higher energy and the other two will be further stabilised. The result is shown on figure 2.4.

|
Octahedral |
square planar |
Figure 2.4: Crystal field splitting diagram for a metal in square planar and octahedral ligand fields.
According to the diagrams above (figures 2.3 and 2.4), it can be seen that a d9 system will prefer a square planar arrangement to a tetrahedral one, because the total energy will be lower in that case, and the same applies to d7 and d8 metals. Metals with a smaller number of electrons will prefer a tetrahedral geometry. Alternatively, if there is no substantial CF energy involved, the ligands will prefer a tetrahedral geometry because that is the situation where they can be the furthest apart from each other.
hole theory
According to hole theory , a d2 system will behave as a d8 system, but with the energy levels inverted. For instance, a d2 system with octahedral symmetry will be like a d8 system with tetrahedral symmetry. The idea is that the d8 system has 2 holes (because d10 is the full shell) and those behave as electrons.
Likewise a d6 system can be treated as a d4 and so on. This approach facilitates the analysis of spectra because a smaller number of electrons (or holes) can be treated, like interpreting a d7 system based on a d3.
The spectra of d1 compounds, like those of Ti (III), are relatively simple. It would be expected, from the theory just described briefly, that d9 compounds would have an equally simple spectra (because they only have one hole), but unfortunately this is not the case. The d9 ions Ag (II) and Cu (II) have very strong spin-orbit coupling, which makes the spectra of their complexes complicated. Furthermore, these complexes often exhibit Jahn-Teller distortion. It is observed that when the degeneracy of orbitals is broken by spin-orbit coupling, the Jahn-Teller effect is not needed, but in the case of these ions one of these two effects will certainly operate. That is one of the reasons why a more sophisticated theory of electronic excitations is needed to study these systems.