Questões de vestibular e concursos públicos
Raciocínio Lógico - IV
Tabela Verdade(ii)
Aplicações da tabela verdade
Ilustração do teorema de Morgan, visto no capítulo III, que diz:
¬(p ∧ q) = (¬p ∨ ¬q)
Vamos novamente fazer uma tabela para p ∧ q, mas desta vez com uma coluna extra para ¬(p ∧ q), que é a negação de p ∧ q, portanto o que é V torna-se F e vice-versa:
p |
q |
p∧ q |
¬(p ∧ q) |
V |
V |
V |
F |
V |
F |
F |
V |
F |
V |
F |
V |
F |
F |
F |
V |
Agora façamos uma tabela para (¬p ∨ ¬q):
p |
q |
¬p |
¬q |
¬p ∨ ¬q |
V |
V |
F |
F |
F |
V |
F |
F |
V |
V |
F |
V |
V |
F |
V |
F |
F |
V |
V |
V |
O resultado é o mesmo da tabela anterior e portanto as duas proposições são equivalentes!
Exemplos - questões de concurso:
1)
Maria está escrevendo uma mensagem a ser enviada por e-mail. Um dos trechos da mensagem traz a seguinte proposição: “Beatriz comprou um carro novo ou não é verdade que Beatriz comprou um carro novo e não fez a viagem de férias”.
A partir dos seus conhecimentos, pode-se afirmar que a única alternativa correta é:
Resolução:
p - Beatriz comprou um carro novo
q- Beatriz fez a viagem de férias
Usando símbolos lógicos o enunciado traduz-se assim:
p ∨ ¬ (p ∧ ¬q)
Metade da questão está resolvida. Agora basta escrever a tabela verdade para a expressão acima:
p |
q |
¬q |
p ∧ ¬q |
¬ (p ∧ ¬q) |
p ∨ ¬ (p ∧ ¬q) |
V |
V |
F |
F |
V |
V |
V |
F |
V |
V |
F |
V |
F |
V |
F |
F |
V |
V |
F |
F |
V |
F |
V |
V |
Nota-se que o resultado (coluna mais à direita) é sempre V, quaisquer que sejam os valores de p e q. Isso quer dizer que é uma tautologia.
Alternativa A
2)
Sabendo-se que, para a construção da tabela verdade da proposição (P ∨Q) ↔ (Q ∧R) , a tabela mostrada abaixo normalmente se faz necessária, é correto afirmar que, a partir da tabela mostrada, a coluna correspondente à proposição (P ∨Q) ↔ (Q ∧R) conterá, de cima para baixo e na sequência, os seguintes elementos: V F F F V F F F.
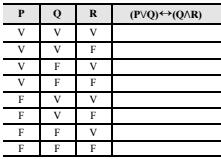
Resolução:
Primeiramente percebam que este é o primeiro exemplo com 3 variáveis: p, q e r. Assim como fizemos com p e q apenas, é necessário escrever todas as combinações posspíveis de valores lógicos V e F para p, q e r. Isto já está feito na tabela dada na pergunta, mas em outros problemas vocè é que terá que fazê-lo. Perceba que temos 3 variávesi e cada uma pode assumir 2 valores (V ou F), portanto o número total de combinações é 23 = 8. A tabela tem 8 linhas.
Resta apenas completar a tabela verdade, da mesma maneira que fizemos acima:
p |
q |
r |
P ∨Q |
Q ∧R |
(P ∨Q) ↔ (Q ∧R) |
V |
V |
V |
V |
V |
V |
V |
V |
F |
V |
F |
F |
V |
F |
V |
V |
F |
F |
V |
F |
F |
V |
F |
F |
F |
V |
V |
V |
V |
V |
F |
V |
F |
V |
F |
F |
F |
F |
V |
F |
F |
V |
F |
F |
F |
F |
F |
V |
Portanto alternativa errado.
Raciocínio lógico - índice de capítulos>>
