Ensino de ciências e matemática bilíngue - inglês / português
Poliedros- Parte 6 - Resolução de questões de vestibular
Resolução de questões de vestibular
1 -(UFMG) Corta-se uma pirâmide regular de base
quadrangular e altura 4 cm por um plano paralelo ao
plano da base, de maneira que os volumes dos dois sólidos
obtidos sejam iguais. A altura do tronco de pirâmide
obtido é, em centímetros,
a) 1
b) 4- 2 3√4
c) 2
d) 4 - 3√2
e) 4 - 4√2
Este é um problema interessante. À primeira vista parece difícil, mas conhecendo-se as relações de semelhança na pirâmide ele é simples:
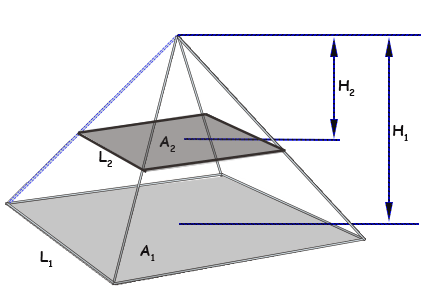
Chamaremos de V1 o volume total da pirâmide e V2 o volume da pirâmide pequena desenhada acima.
Se o volume do tronco de pirâmide (V1 - V2) deve ser igual ao V1, resulta que V2= 2*V1.
Pela fórmula de semelhança sabemos que V2/V1 = H23 / H13
Temos H1 = 4 e H2 = 4 - h
Onde h é a altura que buscamos.
Substituindo os valores:
V2/V1 = 1/2 = (4-h/4)3
3√2 = 4 / 4-h
4-h = 4 / 3√2
Agora basta eliminar este radical do denominador, multiplicando o numerador e o denominador por 3√4
4- h = 4 3√4 / 2 ⇒ h = 4 - 2 3√4
2 - (FUVEST-SP) A figura a seguir representa uma pirâmide
de base triangular ABC e vértice V. Sabe-se que ABC e
ABV são triângulos equiláteros de lado a, e que M é o
ponto médio do segmento AB. Se a medida do ângulo
VMC é 60º, então o volume da pirâmide é ?

a) a3√3/4
b)a3√3/8
c)a3/12
d)a3√3/16
e)a3√3/18
Usaremos a fórmula do volume da pirâmide, base x altura / 3.
A área da base é fácil de calcular: é a área do triângulo equilátero de lado a : a2√3/4 .
Agora resta calcular a altura da pirâmide. O segmento VM representa a altura do triângulo equilátero, que sabemos ser a √3 / 2. A altura da pirâmide pode então ser calculada a partir do triângulo:
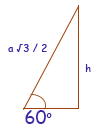
sin 60 = √3 / 2 = h / (a√3 / 2) ⇒ h = 3a / 4
Finalmente, base x altura / 3 = (a2√3/4 * 3a / 4) / 3 = a3√3/16
3 - (FUVEST-SP) Qual a altura de uma pirâmide quadrangular
que tem as oito arestas iguais a √2?
a) 1 b) √1,5 c) √2 c) √2,5 e) √3
Primeiro calculamos a apótema:
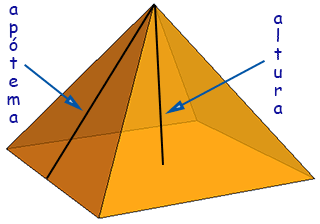
Considerando o triângulo isósceles de lados √2, a apótema é a altura deste triângulo e portanto
apótema = √6 / 2
Agora usa-se Pitágoras para o triângulo formado pela apótema e a altura da pirâmide:
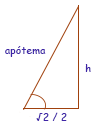
e encontra-se que h = 1.
