Ensino de ciências e matemática bilíngue - inglês / português
Poliedros- Parte 2 - Pirâmides
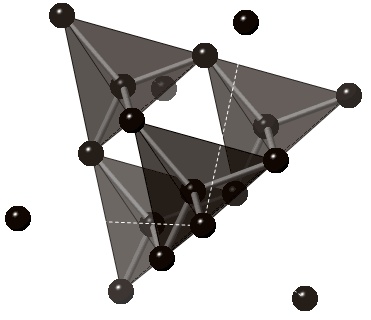
Estrutura cristalina do diamante
Introdução
As pirâmides são formas que sempre causaram fascinação, por milhares de anos. Além das famosas pirâmides do Egito, que são as maiores de todas, existem pirâmides por todos os continentes, construídas por diversas civilizações. Tanta é a perfeição delas que acredita-se que formam construídas com o auxílio de seres extra-terrestres.
Aqui no nosso estudo pirâmides também terão destaque, pois elas caem com muita frequência nas questões de vestibulares.
Pirâmides
As pirâmides podem ter diferentes polígonos como base. Mostrarei aqui 3 exemplos, a pirâmide com base triangular - também chamada de tetraedro, a pirâmide com base quadrada - tipo das do Egito e é a que será mais estudada aqui, e finalmente a pirâmide de base pentagonal. Figura 1 mostrou esses três tipos juntamente com as respectivas planificações (todos os lados no mesmo plano). Nota-se que o tetraedro abaixo é constituído de polígonos iguais (triângulos equiláteros) e por isso é classificado como poliedro regular. Veremos mais adiante que só existem 5 poliedros regulares.
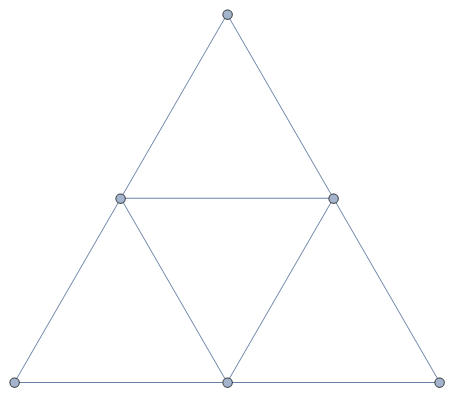
Tetraedro
Pirâmide de base quadrada
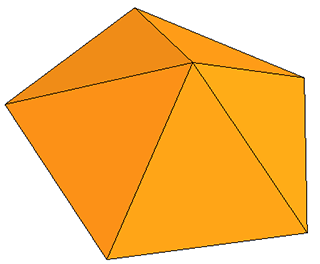
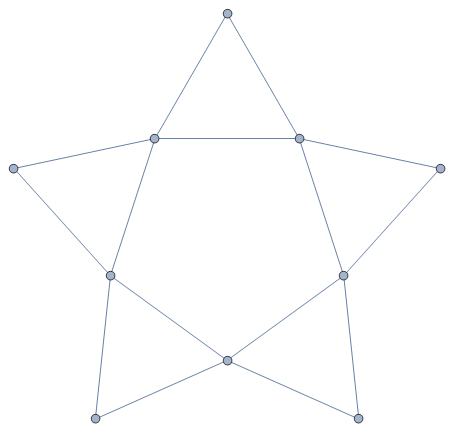
Pirâmide de base pentagonal
Figura 1 - Três tipos de pirâmides, com diferentes polígonos na base, acompanhadas de suas planificações
No caso dos prismas a altura era a distância entre os dois polígonos paralelos. No caso da pirâmide a altura é a distância entre o vértice e a base. A pirâmide tem vários vértices, como todo poliedro, mas quando nos referimos ao "vértice da pirâmide", nos referimos ao vértice superior (figura 2), o qual é unido a todas as faces laterais.
Chamamos de pirâmide regular aquela em que a base é um polígono regular, ou seja, que possui todos os lados congruentes (iguais). Nesse caso a projeção ortogonal do vértice incidirá sobre o centro da base (e esta distância será a altura).
A pirâmide regular possui uma particularidade, que é a distância chamada de apótema: Chama-se apótema de uma pirâmide regular a altura (relativa ao lado da base) de uma face lateral (figura 2).
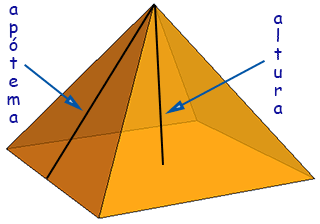
Figura 2 - Altura e apótema da pirâmide
Aplicações na química
Sabe-se que em química o conhecimento da geometria das moléculas é muito importante. As proteínas, por exemplo, têm formas tridimensionais complexas e a menor alteração destas impede o seu funcionamento.
A forma tetraédrica da molécula de metano, com carbono no centro do poliedro e um hidrogênio em cada vértice é bem conhecida de todos. Até mesmo a molécula de água é tetraédrica, com oxigênio no centro, 2 hidrogênios e 2 pares de elétrons ocupando os 4 vértices.
A estrutura cristalina do diamante também apresenta geometria tetraédrica.
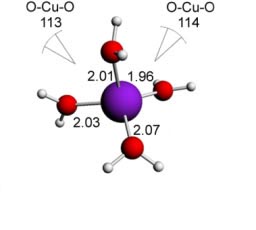
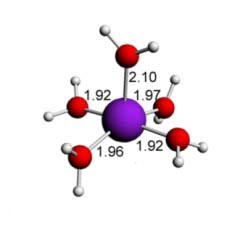
Na química de metais de transição as formas poliédricas são também muito presentes, inclusive para explicar as diversas e lindas cores que são produzidas. Alguns tais complexos (compostos de coordenação) são mostrados abaixo . Percebam que os poliedros nesses casos são ligeiramente distorcidos . Os comprimentos e ângulos das ligações químicas são também mostrados, nestes complexos de cobre e água:
Cu(I) (H2O)4
Tetraedro (distorcido)
Cu(II) (H2O)5
pirâmide de base quadrada (distorcida)
Figura 3 - Compostos de coordenação
A casa da pirâmide em São Tomé das Letras-MG tem suas paredes construídas com pedras locais, sem uso de cimento, e possui uma pirâmide quadrada como teto. A pirâmide é usada aqui para adicionar ao caráter místico e misterioso do local:
Parte 3 - Octaedro, dodecaedro, icosaedro
Parte 4 - Fórmulas, definições e cálculos
Parte 5 - Questões de vestibular